See Saturn as Galileo did!
Altissimum planetam tergeminum observavi («I saw the most distant planet triple-bodied») wrote Galileo about his observations of Saturn in 1610. How could he initially come to such a conclusion? Failure to distinguish the rings is generally attributed to the limited image quality of his telescope at the time. But searching on the web, I found illustrations intended to demonstrate this optical illusion unconvincing, and thought a more plausible simulation could be done.
 Using Celestia I generated an RGB colour image of Saturn seen from Earth at the end of July 1610. The angular equatorial diameter of Saturn was then 18.8". Pixels in the full image measure 0.145"×0.145".
Using Celestia I generated an RGB colour image of Saturn seen from Earth at the end of July 1610. The angular equatorial diameter of Saturn was then 18.8". Pixels in the full image measure 0.145"×0.145".
 Galileo observed Saturn probably with a telescope like the one shown on the left, for which the effective aperture diameter is about 15mm (the objective diameter is 37mm, but the aperture is reduced with a cardboard diaphragm to reduce the amount of optical aberrations).
Galileo observed Saturn probably with a telescope like the one shown on the left, for which the effective aperture diameter is about 15mm (the objective diameter is 37mm, but the aperture is reduced with a cardboard diaphragm to reduce the amount of optical aberrations).
 Assuming the seeing disk full-width at half-maximum was 2" during the observations, the corresponding point spread function (PSF) can be easily simulated with Skymaker for the three visual bands (red, green, blue).
Assuming the seeing disk full-width at half-maximum was 2" during the observations, the corresponding point spread function (PSF) can be easily simulated with Skymaker for the three visual bands (red, green, blue).
IMAGE_SIZE 512 # Width,[height] of the output frame
IMAGE_TYPE PSF_FULLRES # PUPIL_REAL,PUPIL_IMAGINARY,PUPIL_MODULUS,
# PUPIL_PHASE,PUPIL_MTF,PSF_MTF,PSF_FULLRES,
# PSF_FINALRES,SKY_NONOISE,SKY,GRID
# or GRID_NONOISE
PIXEL_SIZE 0.145 # Pixel size in arcsec.
SEEING_FWHM 2.0 # FWHM of seeing in arcsec (incl. motion)
PSF_OVERSAMP 1 # Oversampling factor / final resolution
M1_DIAMETER 0.015 # Diameter of the primary mirror (in meters)
M2_DIAMETER 0.0 # Obstruction diam. from the 2nd mirror in m.
ARM_COUNT 0 # Number of spider arms (0 = none)
WAVELENGTH 0.45 # Average wavelength analysed (microns)
p(:,:,1) = double(imread('psf_r.fits'));
p(:,:,2) = double(imread('psf_v.fits'));
p(:,:,3) = double(imread('psf_b.fits'));
a2 = zeros(2048,2048,3);
p2 = zeros(2048,2048,3);
a2((2048-824)/2+1:(2048+824)/2,(2048-1440)/2+1:(2048+1440)/2,:) = a.^2.2;
p2((2048-1024)/2+1:(2048+1024)/2,(2048-1024)/2+1:(2048+1024)/2,:) = p;
b2 = ifft2(fft2(a2).*fft2(fftshift(p2)));
b = abs(b2((2048-768)/2+1:(2048+768)/2,(2048-768)/2+1:(2048+768)/2,:)).^0.45;
imwrite(uint8(b),'saturnc.png');
 The result (shown on the right) should be a good approximation of what Galileo must have seen in 1610. Despite the blurring, the first null of the Airy pattern provides a clear separation between the planet disk and the ring ansae, increasing the impression of a triple system.
The result (shown on the right) should be a good approximation of what Galileo must have seen in 1610. Despite the blurring, the first null of the Airy pattern provides a clear separation between the planet disk and the ring ansae, increasing the impression of a triple system.





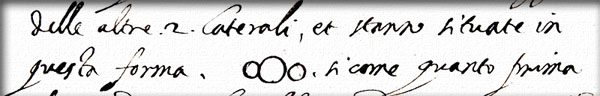
One Comment